Blog Information

• Posted By : The Spring Store
• Posted On : Feb 21, 2025
• Views : 2
• Category : General
• Description : Springs are all around you, from the tiny ones inside pens to massive ones in machinery. While they come in various shapes and sizes, they all share a fundamental property. A higher spring constant means a stiffer spring, while a lower spring constant means a more flexible one. Understanding the spring constant and its different types can help you understand how springs behave under different conditions.

Overview

• Springs are all around you, from the tiny ones inside pens to massive ones in machinery. While they come in various shapes and sizes, they all share a fundamental property. A higher spring constant means a stiffer spring, while a lower spring constant means a more flexible one. Understanding the spring constant and its different types can help you understand how springs behave under different conditions.

   

  What Is Spring Constant?

  The spring constant “k defines the absolute force needed to compress or stretch such elastic objects. A spring constant provides essential information needed to predict the reaction of springs when undergoing deformation. In Hooke's Law, both the force on a spring and its displacement correspond to each other through the spring constant. The formula is simple:

   

  F = k x

  The relationship between spring force "F" and spring constant "k" and displacement "x" of the spring rest position remains direct.

   

  Types of Springs

  1. Linear Springs

  Linear springs represent the basic spring structure whose applied force shows a proportional relationship to their displacement. According to Hooke's Law, the required force will double whenever you double-stretch or compress the spring. These springs serve diverse applications since they appear in mattress coils as well as car suspension systems.

   

  

   

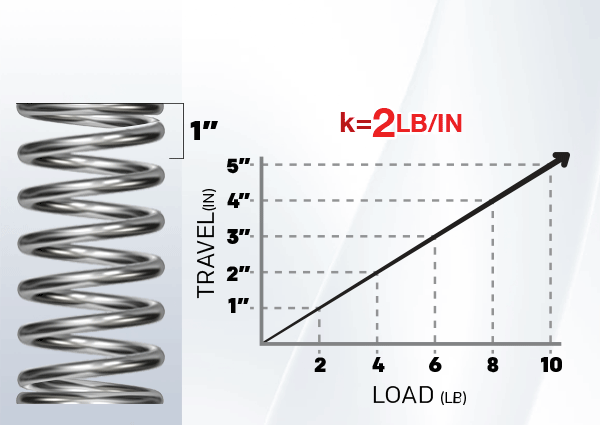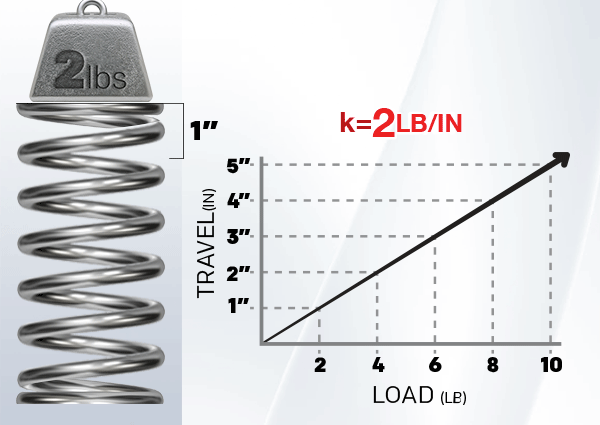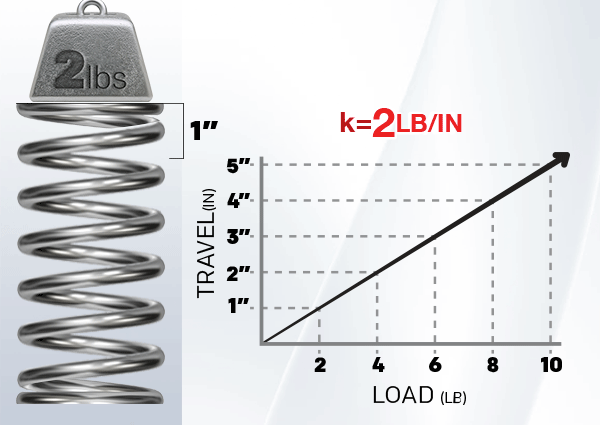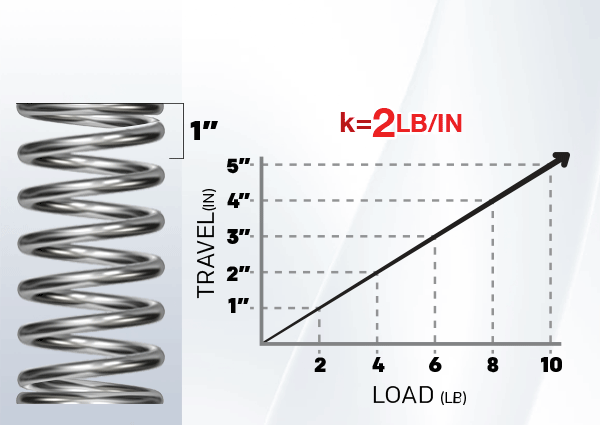
  2. Torsion Springs

  The axis becomes its centre as these springs deviate from their motion rather than facing expansion or contraction. The twisting motion enables them to store energy; therefore, they appear in everyday objects such as clothes pins and garage doors. These springs possess a spring constant, which relates to rotational angle measurements instead of measuring changes in flax size.

   

  3. Constant Force Springs

  The spring's characteristic sets it apart since it creates consistent force throughout its stretch. Linear springs differ from these springs because they do not modify the amount of force output during stretching. The mechanisms that incorporate retractable tape measures alongside window blinds depend on the function of these types of springs. The special constant force spring type produces almost constant force through its unique coil arrangement.

   

  4. Bellville Springs

  The design of these heavy-duty springs appears as stacked washers in series for managing substantial loads. Under pressure, these components show compression elasticity while sustaining high resistance to additional compression.

   

  5. Cylindrical Springs

  Linear springs with higher load capacity serve purposes similar to their standard versions. Different kinds of mechanical systems make use of compression and tension springs.

   

  

   

  6. Flat Springs

  Flat-shaped leaf springs serve various applications and functions for shock absorption and energy storage.

   

  Effective Spring Constant

  Multiple springs used together need an effective spring constant, which appears when they are connected in series or parallel compositions. You can determine this effective spring constant through the systematic combination of each separate spring constant. When put in a parallel arrangement, the spring constant strengthens, while when placed in a series, it gets weaker. Pertaining to multiple spring mechanics, this concept enables people to understand their collective behaviour.

   

  The formula for the spring constant

  The formula for the spring constant F = k x stays the same, although the type of spring, along with its usage, influences the specific calculation of k. The measurement of the spring constant amounts to newtons per meter (N/m) because it defines the force needed to achieve a single meter of displacement.

   

  Spring Constant Calculator & Units

  When in need of simplification, you should use a spring constant calculator. The tools allow users to enter force and displacement values to determine the spring constant quickly. The spring constant measurement expresses itself through the unit for spring constant, N/m (newtons per meter).

   

  Conclusion

  Understanding the spring constant is key to working with springs, whether you're designing mechanical systems or simply trying to understand how they function.